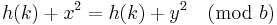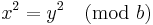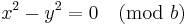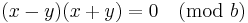Quadratic probing
Quadratic probing is a scheme in computer programming for resolving collisions in hash tables. It is an open addressing method to handle overflows after a collision takes place in some bucket of a hash table. Quadratic probing operates by taking the original hash value and adding successive values of an arbitrary quadratic polynomial to the starting value. The form of the equation is 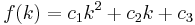 . The function used might even be
. The function used might even be 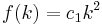 if
if 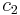 and
and 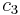 are taken as zero. In this case, suppose a cell H is reached but is occupied, then the next sequence of cells to be examined would be
are taken as zero. In this case, suppose a cell H is reached but is occupied, then the next sequence of cells to be examined would be 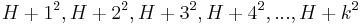 . Linear Probing, instead, would examine the sequence
. Linear Probing, instead, would examine the sequence 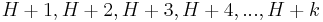 . This would result in primary clustering and the larger the cluster grows, lesser will be the search efficiency for those items. Quadratic probing can be a more efficient algorithm in a closed hash table, since it better avoids the clustering problem that can occur with linear probing, although it is not immune. It also provides good memory caching because it preserves some locality of reference; however, linear probing has greater locality and, thus, better cache performance. Quadratic probing is used in the Berkeley Fast File System to allocate free blocks. The allocation routine chooses a new cylinder-group when the current is nearly full using quadratic probing, because of the speed it shows in finding unused cylinder-groups.
. This would result in primary clustering and the larger the cluster grows, lesser will be the search efficiency for those items. Quadratic probing can be a more efficient algorithm in a closed hash table, since it better avoids the clustering problem that can occur with linear probing, although it is not immune. It also provides good memory caching because it preserves some locality of reference; however, linear probing has greater locality and, thus, better cache performance. Quadratic probing is used in the Berkeley Fast File System to allocate free blocks. The allocation routine chooses a new cylinder-group when the current is nearly full using quadratic probing, because of the speed it shows in finding unused cylinder-groups.
Contents |
Quadratic Function
Let 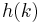 be a hash function that maps an element
be a hash function that maps an element  to an integer in
to an integer in ![[0,m-1]](/2012-wikipedia_en_all_nopic_01_2012/I/e0e830d0094467566642d75777f9f1f6.png) , where
, where  is the size of the table. Let the
is the size of the table. Let the  th probe position for a value
th probe position for a value  be given by the function
be given by the function 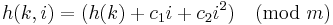 , where
, where 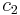 ≠ 0. If
≠ 0. If 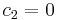 , then
, then 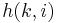 degrades to a linear probe. For a given hash table, the values of
degrades to a linear probe. For a given hash table, the values of 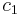 and
and 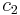 remain constant.
remain constant.
Examples:
- If
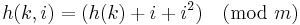 , then the probe sequence will be
, then the probe sequence will be 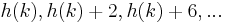
- For
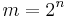 , a good choice for the constants are
, a good choice for the constants are 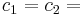 1/2, as the values
1/2, as the values 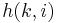 for
for  in
in ![[0,m-1]](/2012-wikipedia_en_all_nopic_01_2012/I/e0e830d0094467566642d75777f9f1f6.png) are all distinct. This leads to a probe sequence of
are all distinct. This leads to a probe sequence of 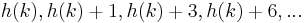 where the values increase by
where the values increase by 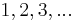 .
. - For prime
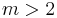 , most choices of
, most choices of 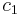 and
and 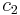 will make
will make 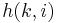 distinct for
distinct for  in
in ![[0, (m-1)/2]](/2012-wikipedia_en_all_nopic_01_2012/I/9f5a3eab53b6dba818e9aa96e53fc26a.png) . Such choices include
. Such choices include 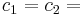 1/2,
1/2, 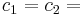 1, and
1, and 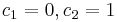 . Because there are only about m/2 distinct probes for a given element, it is difficult to guarantee that insertions will succeed when the load factor is > 1/2.
. Because there are only about m/2 distinct probes for a given element, it is difficult to guarantee that insertions will succeed when the load factor is > 1/2.
Quadratic Probing Insertion
The problem, here, is to insert a key at an available key space in a given Hash Table using quadratic probing.[1]
Algorithm to Insert key in Hash Table
1. Get the key k
2. Set counter j = 0
3. Compute hash function h[k] = k % SIZE
4. If hashtable[h[k]] is empty
(4.1) Insert key k at hashtable[h[k]]
(4.2) Stop
Else
(4.3) The key space at hashtable[h[k]] is occupied, so we need to find the next available key space
(4.4) Increment j
(4.5) Compute new hash function h[k] = ( k + j * j ) % SIZE
(4.6) Repeat Step 4 till j is more than SIZE of hash table
5. The hash table is full
6. Stop
C function for Key Insertion
int quadratic_probing_insert(int *hashtable, int key, int *empty) { /* hashtable[] is an integer hash table; empty[] is another array which indicates whether the key space is occupied; If an empty key space is found, the function returns the index of the bucket where the key is inserted, otherwise it returns (-1) if no empty key space is found */ int j = 0, hk; hk = key % SIZE; while(j < SIZE) { if(empty[hk] == 1) { hashtable[hk] = key; full[hk] = 1; return (hk); } j++; hk = (key + j * j) % SIZE; } return (-1); }
Example to Insert key in Hash Table
There are two possible cases to consider:
- Key space at position h[k] is empty : Insert the key at the position.
- Key space at position h[k] is occupied: Compute the next hash function h[k].
Consider a hash table initially containing some elements.
Suppose we want to insert a key 10 in the hash table.
h[k] = 10 % 8 = 2
Slot 2 being occupied the hash function will search for new available key space.
h[k] = ( k + j * j ) % SIZE
h[k] = ( 2 + 1 * 1 ) % 8 = 3
Slot 3 is also occupied, so the hash function will search for next available key space.
h[k] = ( 2 + 2 * 2 ) % 8 = 6
Slot 6 is empty, so key will be inserted here.
Quadratic Probing Search
Algorithm to Search Element in Hash Table
1. Get the key k to be searched
2. Set counter j = 0
3. Compute hash function h[k] = k % SIZE
4. If the key space at hashtable[h[k]] is occupied
(4.1) Compare the element at hashtable[h[k]] with the key k.
(4.2) If they are equal
(4.2.1) The key is found at the bucket h[k]
(4.2.2) Stop
Else
(4.3) The element might be placed at the next location given by the quadratic function
(4.4) Increment j
(4.5) Compute new hash function h[k] = ( k + j * j ) % SIZE
(4.6) Repeat Step 4 till j is greater than SIZE of hash table
5. The key was not found in the hash table
6. Stop
C function for Key Searching
int quadratic_probing_search(int *hashtable, int key, int *empty) { /* If the key is found in the hash table, the function returns the index of the hashtable where the key is inserted, otherwise it returns (-1) if the key is not found */ int j = 0, hk; hk = key % SIZE; while(j < SIZE) { if((empty[hk] == 0) && (hashtable[hk] == key)) return (hk); j++; hk = (key + j * j) % SIZE; } return (-1); }
Limitations
[2] For linear probing it is a bad idea to let the hash table get nearly full, because performance is degraded as the hash table gets filled. In the case of quadratic probing, the situation is even more drastic. There is no guarantee of finding an empty cell once the table gets more than half full, or even before the table gets half full if the table size is not prime. This is because at most half of the table can be used as alternative locations to resolve collisions. If the hash table size is b (a prime greater than 3), it can be proven that the first 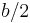 alternative locations including the initial location h(k) are all distinct and unique. Suppose, we assume two of the alternative locations to be given by
alternative locations including the initial location h(k) are all distinct and unique. Suppose, we assume two of the alternative locations to be given by 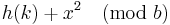 and
and 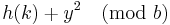 , where 0 ≤ x, y ≤ (b / 2). If these two locations point to the same key space, but x ≠ y. Then the following would have to be true,
, where 0 ≤ x, y ≤ (b / 2). If these two locations point to the same key space, but x ≠ y. Then the following would have to be true,
As b (table size) is a prime greater than 3, either (x - y) or (x + y) has to be equal to zero. Since x and y are unique, (x - y) cannot be zero. Also, since 0 ≤ x, y ≤ (b / 2) , (x + y) cannot be zero.
Thus, by contradiction, it can be said that the first (b / 2) alternative locations after h(k) are unique. So an empty key space can always be found as long as at most (b / 2) locations are filled, i.e., the hash table is not more than half full.